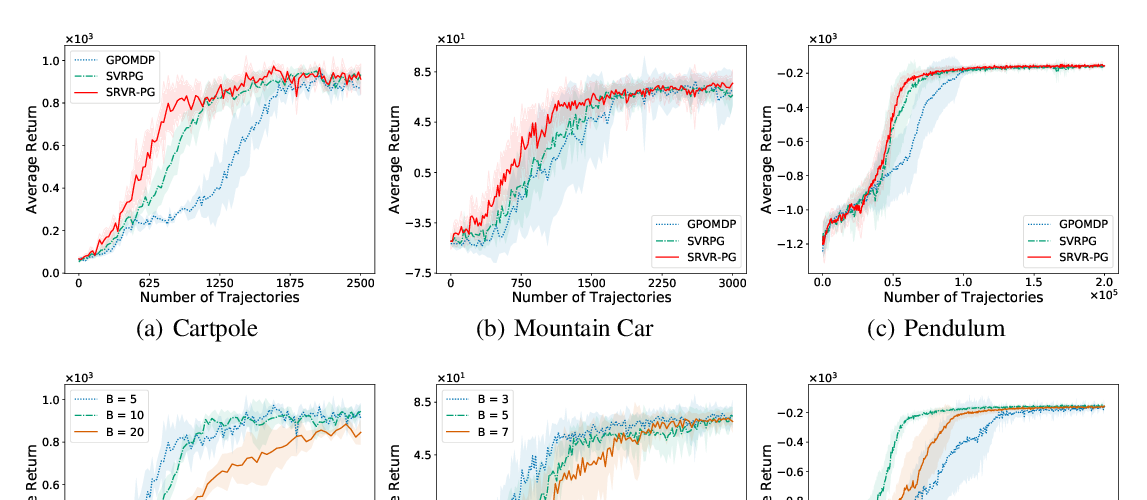
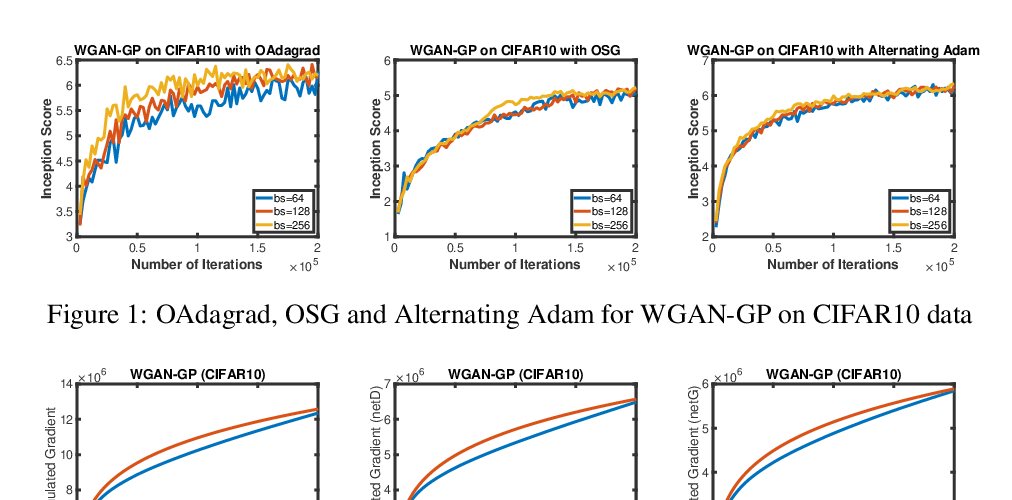
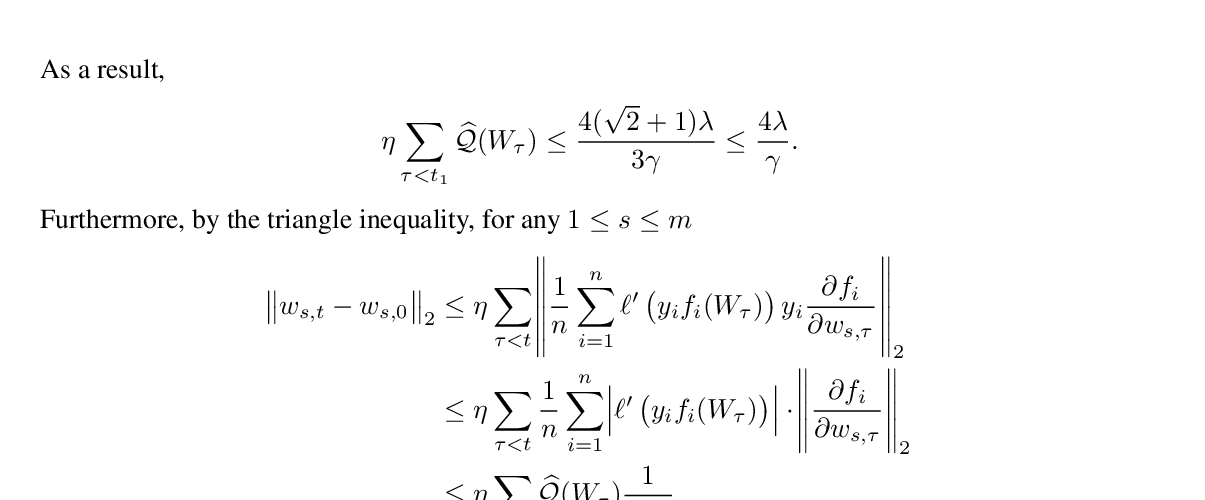Abstract:
A fundamental question in reinforcement learning is whether model-free algorithms are sample efficient. Recently, Jin et al. (2018) proposed a Q-learning algorithm with UCB exploration policy, and proved it has nearly optimal regret bound for finite-horizon episodic MDP. In this paper, we adapt Q-learning with UCB-exploration bonus to infinite-horizon MDP with discounted rewards \emph{without} accessing a generative model. We show that the \textit{sample complexity of exploration} of our algorithm is bounded by $\tilde{O}({\frac{SA}{\epsilon^2(1-\gamma)^7}})$. This improves the previously best known result of $\tilde{O}({\frac{SA}{\epsilon^4(1-\gamma)^8}})$ in this setting achieved by delayed Q-learning (Strehlet al., 2006),, and matches the lower bound in terms of $\epsilon$ as well as $S$ and $A$ up to logarithmic factors.