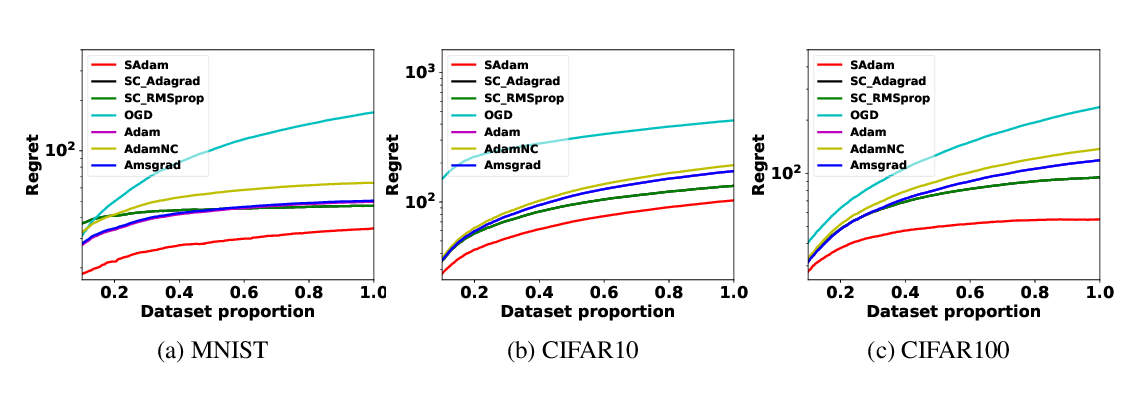
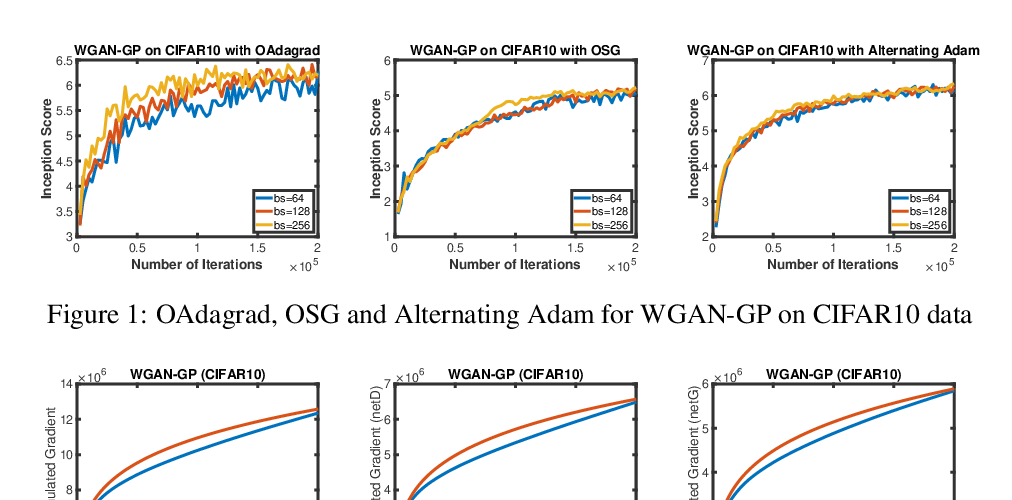
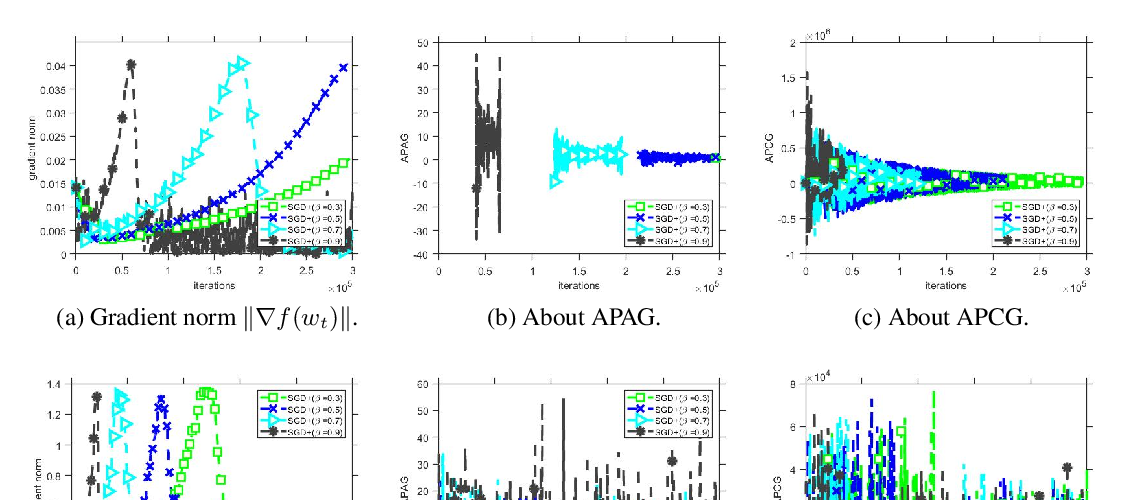
Abstract:
We consider the problem of unconstrained minimization of a smooth objective
function in $\mathbb{R}^d$ in setting where only function evaluations are possible. We propose and analyze stochastic zeroth-order method with heavy ball momentum. In particular, we propose, SMTP, a momentum version of the stochastic three-point method (STP) Bergou et al. (2019). We show new complexity results for non-convex, convex and strongly convex functions. We test our method on a collection of learning to continuous control tasks on several MuJoCo Todorov et al. (2012) environments with varying difficulty and compare against STP, other state-of-the-art derivative-free optimization algorithms and against policy gradient methods. SMTP significantly outperforms STP and all other methods that we considered in our numerical experiments. Our second contribution is SMTP with importance sampling which we call SMTP_IS. We provide convergence analysis of this method for non-convex, convex and strongly convex objectives.