Abstract:
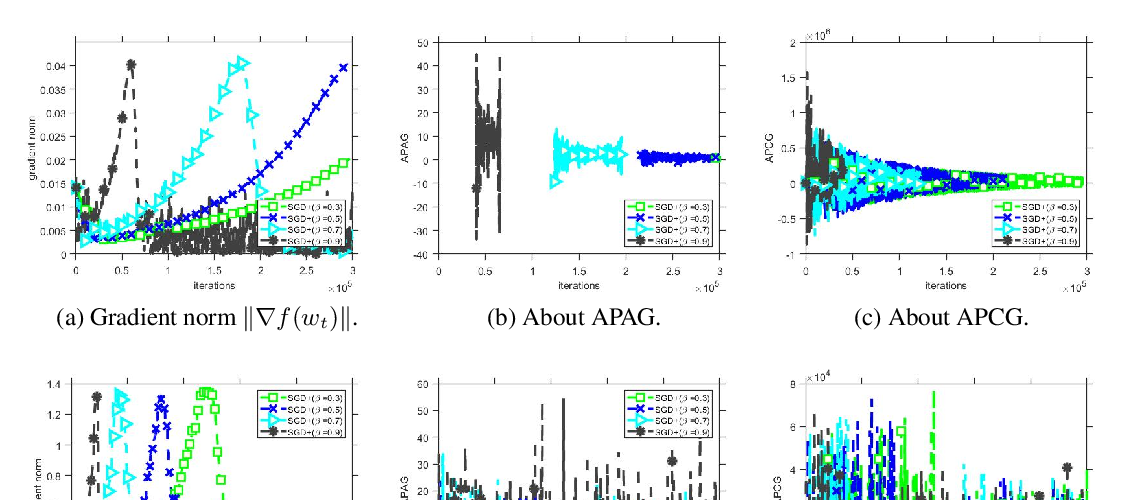
Homotopy methods, also known as continuation methods, are a powerful mathematical tool to efficiently solve various problems in numerical analysis, including complex non-convex optimization problems where no or only little prior knowledge regarding the localization of the solutions is available.
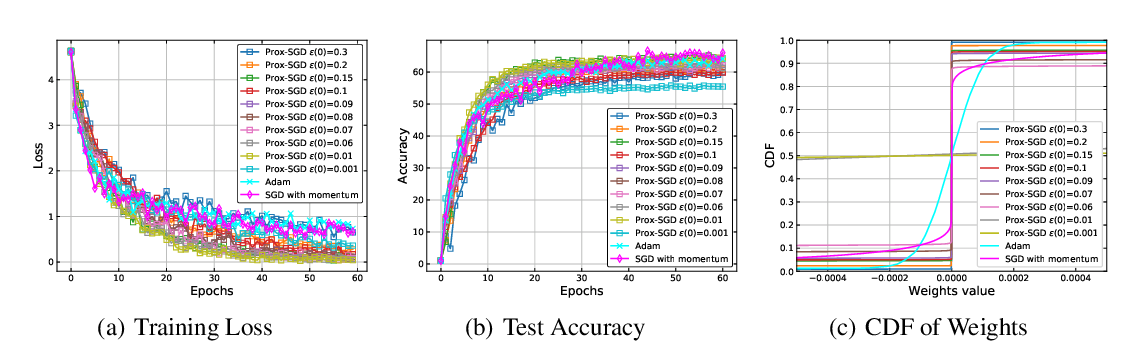
In this work, we propose a novel homotopy-based numerical method that can be used to transfer knowledge regarding the localization of an optimum across different task distributions in deep learning applications. We validate the proposed methodology with some empirical evaluations in the regression and classification scenarios, where it shows that superior numerical performance can be achieved in popular deep learning benchmarks, i.e. FashionMNIST, CIFAR-10, and draw connections with the widely used fine-tuning heuristic. In addition, we give more insights on the properties of a general homotopy method when used in combination with Stochastic Gradient Descent by conducting a general local theoretical analysis in a simplified setting.