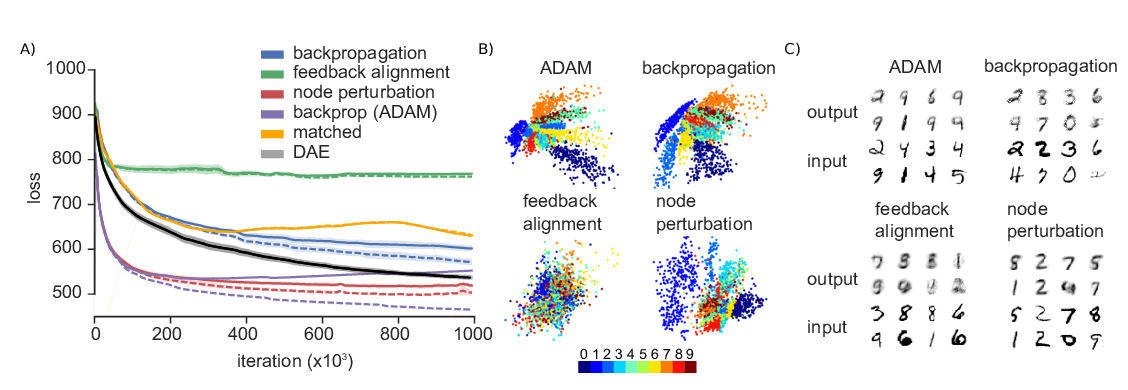
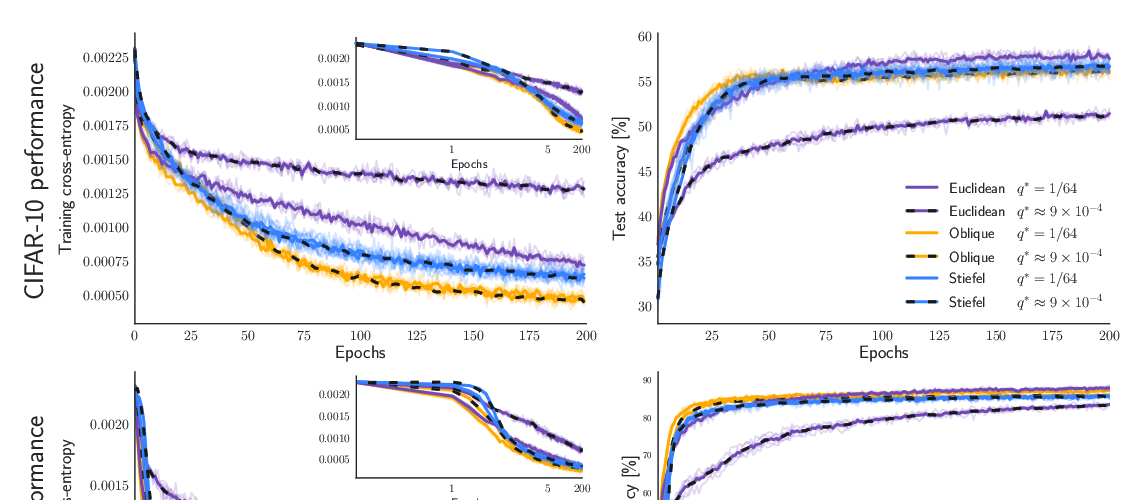
Abstract:
In artificial neural networks trained with gradient descent, the weights used for processing stimuli are also used during backward passes to calculate gradients. For the real brain to approximate gradients, gradient information would have to be propagated separately, such that one set of synaptic weights is used for processing and another set is used for backward passes. This produces the so-called "weight transport problem" for biological models of learning, where the backward weights used to calculate gradients need to mirror the forward weights used to process stimuli. This weight transport problem has been considered so hard that popular proposals for biological learning assume that the backward weights are simply random, as in the feedback alignment algorithm. However, such random weights do not appear to work well for large networks. Here we show how the discontinuity introduced in a spiking system can lead to a solution to this problem. The resulting algorithm is a special case of an estimator used for causal inference in econometrics, regression discontinuity design. We show empirically that this algorithm rapidly makes the backward weights approximate the forward weights. As the backward weights become correct, this improves learning performance over feedback alignment on tasks such as Fashion-MNIST and CIFAR-10. Our results demonstrate that a simple learning rule in a spiking network can allow neurons to produce the right backward connections and thus solve the weight transport problem.