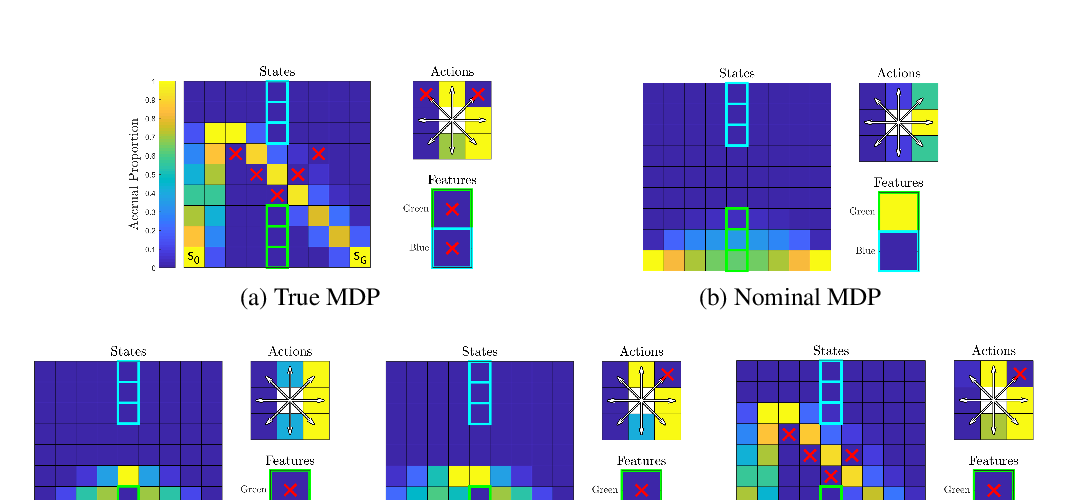
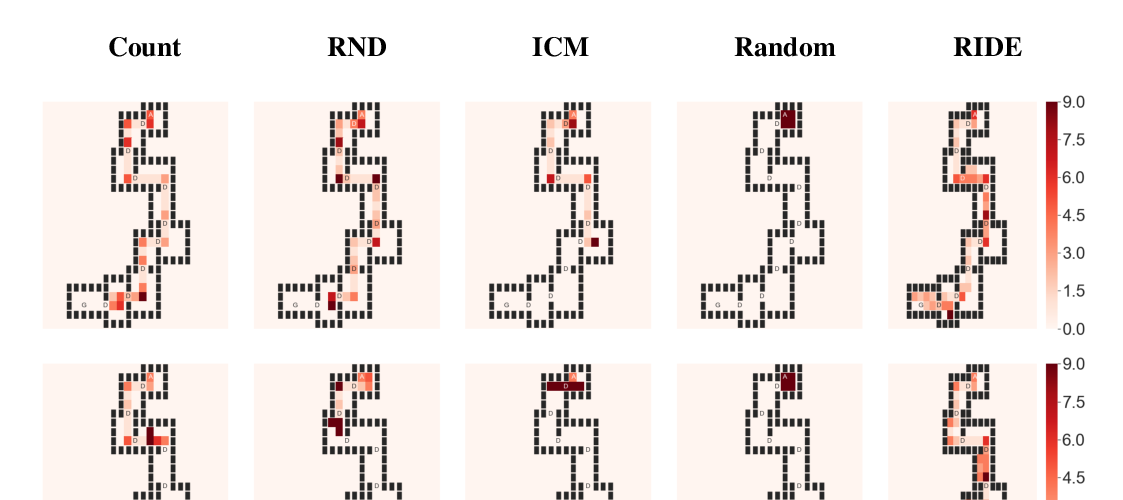
Abstract: We humans have an innate understanding of the asymmetric progression of time, which we use to efficiently and safely perceive and manipulate our environment. Drawing inspiration from that, we approach the problem of learning an arrow of time in a Markov (Decision) Process. We illustrate how a learned arrow of time can capture salient information about the environment, which in turn can be used to measure reachability, detect side-effects and to obtain an intrinsic reward signal. Finally, we propose a simple yet effective algorithm to parameterize the problem at hand and learn an arrow of time with a function approximator (here, a deep neural network). Our empirical results span a selection of discrete and continuous environments, and demonstrate for a class of stochastic processes that the learned arrow of time agrees reasonably well with a well known notion of an arrow of time due to Jordan, Kinderlehrer and Otto (1998).